Article based on a lecture kept at the International Yoga Congress, Bucharest, 25th of November 2012 by Johanes Dragonoff.
Contents:
- Objective
- A brief history of concepts regarding infinity
- Infinities in Mathematics
- Runaway infinities
- Logic bomb of 1931
- The Biggest of them all
- Actual infinities, physical infinities and infinities in physics
- Psychological and spiritual considerations
- Holographic Infinity
- Further spiritual considerations – infinity breaking out of the limits of mathematics
- Touching the Void
- Reflection Principle
Objective
The objective of this article is to bring understanding and clarity for the mind regarding concepts of infinity and with this clarity to create space in the mind (space between thoughts) to allow a deeper intuitive awareness of infinity thus helping to achieve the fundamental goal of yoga:
Expansion of one’s consciousness from finite to infinite.
Any true spiritual approach includes in its objective this radical shift of perspective; stepping out from a limited view and letting go of identification with finite structures in order to move into a fundamentally new state of being without borders or limitations, with complete openness, thus:
Embracing Infinity
or
Total Freedom.
The Tantric system will eventually offer a reconciliation of these two aspects - finite and infinite - into one coherent Whole with the holographic model where every part is reflecting Totality and Totality is reflected in all of its parts. For the conceptual, rationalizing mind this seems an impossibility, but with a deeper understanding of infinity this newly discovered ancient principle starts to appear as plausible (as we can see later in this article) and even inevitable.
Studying, clarifying and contemplating the concept of infinity and taking some mental and mathematical leaps from finite to infinite can be considered a step in Jnana yoga if carried out with an open mind that leaves space for intuition and the feeling of mystery.
Jnana yoga characterized by Gregorian Bivolaru:
This apparently paradoxical approach,where reason is actually used to transcend reason
is well known in the Eastern spiritual tradition as JNANA YOGA
or the Way of the Discriminating Intuitive Knowledge.
This is a spiritual path to provide an exquisite metaphysical purity,
starting from some basic mind functioning such as reasoning and discrimination.
Just like the wise, superior use of sexual energy in the tantric methods,
reason can also provide the operation upon some tremendous,
mysterious energies and incredible forces
to lead the wise aspirant to the state of spiritual freedom
whereas the foolish will be tied up in even stronger bounds.
A brief history of concepts regarding infinity
The ancient Greeks used the word Apeiron for infinity. Its meaning is ‘without a perimeter’, ‘without limit’. The Latin based word infinity comes from infinita; no limits, without limits. Sometimes the words limitless and unbounded are used as synonymes to infinity, but these words can also be used with a slightly different meaning. Greeks did not generally accept infinity as something truly existing, not even as a platonic entity. Plato (424-348 BC) himself rejected the concept of (manifested) infinity supporting Pythagoras (569–c.495 BC) in the belief that any given aspect of the universe could be represented by a finite arrangement of natural numbers. For most greek philosophers as well as for some mathematicians even up to present day infinity was only a possibility, a potential infinity of something that is allowed in principle to increase without limit. There were exceptions, like Anaximander (610–c.546 BC), who thought Apeiron as the source and ultimate destiny of all things and elements. Pythagoras held numbers in a very high esteem, of divine origin and character. Things like irrational numbers (e.g. square root of 2) presented a problem because of their unpredictably infinite nature (e.g. in their expression one encounters an endless series of digits without any detectable pattern).
Zeno (495-435 BC) expressed his view about infinitely small divisions in his famous paradoxes (e.g. Achilles and Tortoise). According to him we run into problems if we allow space and time to be divided infinitely. These paradoxes are now easily resolved with sums of infinite series. Infinite sums were used in India in the 15th century to calculate the transcendental number Pi (3.14159265... Pi/4 = 1 - ⅓ + ⅕ - 1/7 + 1/9 …). In Europe this kind of infinity was studied among others by Gottfried Leibniz (1646-1716) who developed together with Isaac Newton (1642-1727) the modern infinitesimal calculus, which became ground for much of the success of mathematics and physics of modern times. In these mathematical tools a variable is allowed to approach infinitely close to a limit value (e.g. limit (1/x) = 0, as x tends to infinity).
Still a rigorous and consistent theory of infinity (or rather infinities) was missing until the ingenious work of Georg Cantor (1845 - 1918). In 1874 he proved that there are several kinds of infinities, in fact infinitely many kinds of infinities.
Infinities in Mathematics
The simplest infinity can be intuitively arrived at by letting the sequence of natural numbers
1, 2, 3, 4, 5, 6, 7, ...
continue without limit.
Until Cantor’s publications in 1870’s it was thought in the western world that all infinity was of this same nature. Cantor proved that indeed the set of all rational numbers (defined as a ratio of two integers, p/q) and the set of all algebraic numbers (solutions to polynomial equations, square roots etc.) have the same infinite size as the set of all natural numbers.
Cantor created modern set theory and he defined numbers with sets and distinguished them in two basic categories: ordinal numbers and cardinal numbers.
He gave a formal definition for the comparison of size extended to infinite amounts; two finite or infinite sets have the same size (same cardinality) if there exists a one-to-one correspondence between them (a bijection). The simpliest, smallest infinity of natural numbers (and rational numbers) Cantor called countable 'infinity' (an infinity that can be 'counted' with natural numbers - at least in principle). He then proved that the set of all real numbers is much bigger in size, that it cannot be counted with natural numbers unlike rational numbers. (see e.g. a proof with the famous diagonal argument that Cantor invented). This new, essentially larger infinity Cantor named uncountable. He called both of these infinities examples of transfinite numbers. He reserved the word infinite to something else (explained later in this article) although many mathematicians do not always make this distinction.
Ordinals
An ordinal number is expressing order or position of a member in an ordered set, e.g. the 5th person in a queue or 26th letter in an alphabet. Whereas a cardinal number is answering the question: how many members there are in a set. With finite numbers these two categories have identical properties but with transfinite numbers their behaviour differs in ways that are not always self-evident to our everyday experience of numbers.
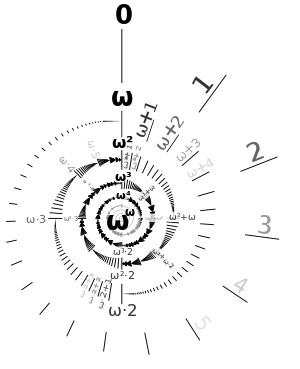
The first transfinite ordinal number Cantor named omega, ω (omega is the last letter in Greek alphabet, meaning also 'great o', o-mega). So ω comes in a sequence after all natural numbers. Yet we can put another transfinite number after it to get a bigger ordinal: ω + 1, and so on. Note that 1 + ω = ω (since we are adding 1 to the beginning of the queue of all natural numbers and ω comes right after them), but ω + 1 > ω since ω + 1 comes after ω, it is in the next position after the sequence of 1, 2, 3, ... ω.
Cantor showed that there are uncountably many countably infinite ordinals.
Some of them are listed here:
ω, ω + 1, ω + 2, …, ω·2, ω·2 + 1, …, ω2, …, ω3, …, ωω, …, ωω^ω …, ε0, ….
ε0 is the first ordinal that satisfies the equation ε0 = ωε0 (epsilon-zero equals omega to the power of epsilon-zero). This means, for example, that ε0 is so big that it cannot be made any bigger with any number* of multiplications of the first infinity, ω. [* any number smaller or equal to itself] - so it is in a way 'beyond multiplication'.

A graphical "matchstick" representation of the ordinal ω². Each stick corresponds to an ordinal of the form ω·m+n where m and n are natural numbers. (from Wikipedia)
Representation of the ordinal numbers up to ωω. Each turn of the spiral represents one power of ω. (from Wikipedia)
Cardinals
The arithmetic behaviour of transfinite cardinals is different.
The first transfinite cardinal is called aleph-zero (aleph is the first letter in Hebrew alphabet).
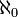 is the size or cardinality of all countable sets, including the set of all natural numbers and also the set of all rational numbers.
is the size or cardinality of all countable sets, including the set of all natural numbers and also the set of all rational numbers.
Any addition to this number with anything we have so far, even with another countably infinite number will produce a number of same cardinality, e.g.:

and same thing happens even if we repeat this adding (countably) infinitely many times, in effect multiplying infinity by infinity, e.g.:

So we can raise aleph-zero to any power and it does not get any bigger.
Making a powerset (a set of all possible subsets) of a given set will however produce a significantly larger set (by cardinality). So the set of all possible subsets of natural numbers is essentially larger than the set of all natural numbers (see the diagonal argument). This radically greater infinity is called aleph-one. This is the cardinality of the set of all real numbers.
This is usually assumed (or rather postulated) to be the cardinality of the so called continuum, a continuous set of points where one can always find a point between any two (separate) points no matter how close they are. Such a continuum is for example space as a set in geometry. Note that also subtracting an infinite part from an aleph-infinity will not change its size and same goes with division: e.g. any limited range of the continuum will have the same infinite size as the original, there are exactly as many real numbers between for example zero and one as there are real numbers in the whole real number axis from -∞ to +∞. Both sets have the cardinality of aleph-one.
From this fundamentally larger infinity of aleph-one (e.g. real numbers) one cannot produce a bigger cardinal infinity by adding or multiplying with other infinities of the same cardinality. So the set of all points on an infinite plane or in n-dimensional infinite space is also having this same cardinality (aleph-one), even if the dimension of space is countably infinite! (For any cardinal infinity x, it holds that xn = x, where n is countable - e.g. aleph-zero). Only when we make another powerset of these transfinite sets do we reach the next transfinite cardinal: aleph-two. This next aleph (aleph-two) is the size of the set of all possible functions, mappings of real numbers to each other and it also expresses the size of the set of all possible geometrical objects.
Runaway infinities
We can form larger and larger cardinal infinities in a similar way with powersets of previous sets without any limit to this process. According to so called generalized continuum hypothesis there are no transfinite cardinals between these aleph numbers, each describing the cardinality of the powerset of its predecessor. There cannot be a largest infinity in this collection, because one can always make a powerset of any previously biggest set and thus get a bigger infinity.
Many contemporary mathematicians objected to Cantor’s ideas and claimed that no actual, definite, well-defined infinities exist and that mathematics should stick to what can be produced in a finite way. C.F.Gauss, who was developing further the infinitesimal calculus said already in 1831:
"I protest against the use of infinite magnitude as something completed, which is never permissible in mathematics. Infinity is merely a way of speaking, the true meaning being a limit which certain ratios approach indefinitely close, while others are permitted to increase without restriction."
All these infinities are indeed a huge challenge to a rational approach to numbers. Consider for example the so called Cantor’s Paradox:
Not only are there infinitely many infinities, but the size of this collection of all infinities is larger than any of those infinities.
Thus when collecting all possible infinities, we encounter a new, larger infinity, larger than any of those collected, which should have already been in that collection of all infinities. This means that the collection of all infinities seems to be something not very well defined or understood. It suggests a new kind of infinity beyond all others.
A note worth mentioning here: In India mathematical studies were for a long time advancing much ahead of Europe and already in 400 BC a work called Surya Prajnapti classified all numbers into three categories: enumerable, innumerable, and infinite, something strikingly similar to Cantor’s concepts over two thousand years later.
With alpeh-one infinity of the real numbers one can make a split into two categories:
- rational and algebraic numbers: a countably infinite (aleph-zero) subset of real numbers - these have a neat formula appealing to the rational mind and
- those irrational real numbers that are called transcendental numbers, numbers that escape a polynomial expression, not being roots of any polynomial equation.
This second part is a dominatingly huge (aleph-one) subset of real numbers. These transcendentals like π (pi), or ϵ (napier, base of natural logarithm) are much more numerous, ubiquitous, dense compared to the rational and algebraic numbers (fractions like 1/3 or roots like √2). One can picture rational and algebraic numbers like very sparsely scattered few ‘islands’ in the vast sea of transcendentals. So the explicit definition or expression of by far most numbers is not reachable by finite operations of simple numbers, they are not allowing expression in closed form, not aching to fully manifest themselves, forever floating beyond easy functional reach in the sea of possibilities. These trancendentals are very difficult to 'catch' - for example after a century of research we still don't know if π + ϵ is a transcendental number even though both π and ϵ are proven to be transcendentals.
All this was dawning on mathematicians towards the end of the 19th century, just before fundamental revolutions in physics took place.
Some years later, in 1931, while theories of relativity had recently been accepted and quantum mechanics was well in the making, a German logician and mystic Kurt Gödel (1906-1978) took up Cantor’s proof with diagonal argument and applied it to logic. Soon the community of logicians were shaken by this hard blow to the hopes for reason and mechanical logic winning over nature's mysteries. Gödel’s incompleteness theorem (first of two) proves that any logic system that includes even the simplest form of infinity (that can work with the set of natural numbers like first order predicate logic) is inevitably incomplete. Incompleteness means that it is not possible to prove all true statements in that system. Second incompleteness theorem proves that the above mentioned system of logic cannot prove its own consistency. For a formal system to be consistent means that no contradictions can be derived from it. If a contradiction arose, the whole system would be useless - it would produce arbitrary statements as truths and would lose all discriminative power.
What Gödel showed was that while logic works fine with finite sets and arguments (propositional logic), as soon as logic tries to embrace infinity - even the simplest kind of infinity of natural numbers - it ceases to be a universally valid tool for uncovering truth, deciding the truth of logical statements. Like the vast sea of unreachable numbers in the infinity of aleph-one, also logic with infinity (first and any higher order predicate logic) includes actually an infinite space of logical statements that cannot all be reached by formally proving them. Not even in principle nor with infinitely powerful computers (see Turing machines). Their truth is left for higher reason, a stroke of genius or intuition to uncover, but for this there is no guarantee. However, Gödel believed that all mathematical problems are solvable by clarifying and deepening the investigation beyond the mechanizing trends of the lower mind. He believed in the power and necessity of logic in philosophical investigations, but this logic needs to be supported by deep and enlightening intuitions.
So mechanical reason and logic can hope to bring at most a few drops of light here and there but never to enlighten the depths of universal possibilities. The more reason tries to expand the horizon of knowing, the more there open up infinitely vaster spaces that are doomed to stay hidden for (and from;) that very reason. It seems this incompleteness is deeply inherent in the analytical approach. Limits of the analytical mind have become clearer and even non-refutable and this seems to be very much what Gödel intended to show - not to put an end to the philosophical inquiries into Truth, but to oppose the modern trend to trivialize, relativize and mechanise this search - a trend that seems to have a major hidden agenda of removing the Absolute Truth altogether from the domain of scientific inquiry.
There is a deep lesson here for people outside the field of logic as well. Theories of relativity and quantum mechanics might fundamentally change the common thinking if our mind could apply those expanded and shifted views to our everyday attitudes, even though the predictions of these theories themselves are not discernible at ordinary non-relativistic and macroscopic scales of perception - for example the notion of quantum entanglement could loosen up deep mental habits of defining everything as separable entities and disconnectable categories. Properly applied, Gödels incompleteness theorems might hit even deeper, uprooting the hidden belief that the infinite reality can be understood and covered by the finite rational mind. Yet we have other tools available, although not so much favoured and cultivated within the last few centuries of scientific revolution. These tools rely on intuition guiding us deeper into seeing the platonic realities and refining abstract thinking to express these intuitions with clarity.
The Biggest of them all
(in the end there can only be One)
So is there an end to the infinite series of ever increasing infinities?
Cantor was contemplating on a new kind of infinity aside from transfinite numbers arising from his set theory and perhaps inspired by it.
He recognized a special infinity of absolute nature; Absolutum or Absolute Infinity, sometimes called (capital) Omega, Ω. (previously we designated the first transfinite ordinal with small omega, ω). This Big Omega is bigger than any of the transfinite cardinals or ordinals and not constructible from these and not definable in any mathematical formalism or otherwise.
Cantor described Absolutum in relation to the manifested reality:
Accordingly I distinguish an eternal uncreated infinity or absolutum which is due to God and his attributes, and a created infinity or transfinitum, which has to be used wherever in the created nature an actual infinity has to be noticed, for example, with respect to, according to my firm conviction, the actually infinite number of created individuals, in the universe as well as on our earth and, most probably, even in every arbitrarily small extended piece of space. One proof is based on the notion of God. First, from the highest perfection of God, we infer the possibility of the creation of the transfinite, then, from his all-grace and splendor, we infer the necessity that the creation of the transfinite in fact has happened. (Georg Cantor: Gesammelte Abhandlungen mathematischen und philosophischen Inhalts. 1932)
Actual infinities, physical infinities and infinities in physics
The mathematical meaning of actual infinity is synonymous with definite, completed, or existentially true infinity. Many mathematicians objected to the way Cantor was considering infinities as platonic objects, existing in themselves and just waiting to be discovered. Even Cantor himself was reluctant to admit the existence of infinitely small numbers used in differential calculus.
The existence of mathematical infinities in this actual sense does not imply their physical manifestation. The question of whether infinite numbers can be considered as true mathematical objects is therefore independent of the question of whether infinite things exist physically in nature.
The question of the finite or infinite nature of the universe, both in the sense of big and small, as well as in respect to both space and time is still open for modern physics. For a long time the universe was thought to be finite in size as well as limited in the sense of the smallest size, consisting of smallest undividable units - atoms. Aristotle's model of finite universe with nine celestial spheres around Earth was the standard view after classical era. Nicholas of Cusa in the the 15th Century argued that the universe was infinite and that the stars were distant suns. Catholic Church tried violently to remove such heresies. Also Giordano Bruno believed in the infinitude of universe:
"Innumerable suns exist; innumerable earths revolve around these suns in a manner similar to the way the seven planets revolve around our sun. Living beings inhabit these worlds."
- On the infinite universe and worlds (Giordano Bruno, 1584)
Bruno was tortured for nine years by the Inquisition in an attempt to make him agree that the universe was finite. He refused to change his views and was burned at a stake in the year 1600.
Current observations and cosmological theories set a limit to the size of the visible universe of some 14 billion (14 000 000 000) light years. But the question still remains open if the geometry of the universe is open or closed, weather the universe is expanding indefinitely or starting at some point to shrink and finally collapse into another singularity or something. Current measurements are suggesting an accelerated expansion without anything in sight to stop this, but the nature of the newly (re-)discovered force causing this expansion (zero-point energy or vacuum energy or ‘ether’) is yet poorly known. According to a theory of one of the leading cosmologists Andrei Linde "our universe is part of a multidimensional fractal and this universe, our cosmic home grows, fluctuates and eternally reproduces itself for all types of life that it can support". This view is in line with the shaivistic concept of Svatantrya, perfect freedom of the creative energy and also with the ideas of René Guénon explained in a chapter below.

Also the question of the smallest unit of space and time is still open. From quantum physics the theories have raised a limit to the smallest possible meaningful extension of space and time (so called Planck scale, approximately 10-35 meters and 10-43 seconds). What lies beneath this scale is a mystery still. A fractal-like geometry is also conceivable, even without lower boundaries.
Modern physics is based on mathematics. In the heart of its analytical tools are differential and integral calculus based largerly on the ideas and formulations by Newton and Leibniz in the 1670's. These rely on infinitesimal scenarios, variables approaching infinitely small or large values, or approaching a target arbitrarily close (reaching thus a so called limit). For many mathematicians infinities are just handy tools, regarded as not really existing, nor problematic or challenging to the philosophical premises. Yet physicist are sometimes bumping into infinities as a result of formulas applied to some specific situations like getting an infinite energy density when approaching the point-like center of an electron that is surrounded by a cloud a virtual photons or the infinite curvature of space around matter that is collapsed into a singularity with the gravitational implosion of a star (black holes). In these situations physicists are drawing a border around infinity, a safety zone to keep the results finite and meaningful (e.g. renormalization in quantum mechanics). Infinities and singularities rising as results from equations would wreck the predictive power and meaningfulness of those equations in similar manner as contradictions would nullify a logical argument (unless indirectly used in reductio ad absurdum). So the concept of infinity provides a powerful tool but also a challenging adversary for the analytic mind.
Psychological and spiritual considerations
A human being usually identifies herself more or less unconsciously with some of the limited structures; body, emotions, thoughts etc. in her being and this prompts a self-preservation mechanism to reject anything smelling radically out of bounds, which infinity certainly can do. Even from the reactions and comments of contemporay mathematicians to the daring leaps of Leibniz, Cantor, Gödel and like, it is possible to sense the play of the mind trying to hide from the immense force of the infinite unknowable. This is especially the case if one has not allowed any space in one's heart for the idea of a 'benevolent infinity' thus basing one's beliefs only on matter, senses, propabilities and a 'cold cosmos'.
Last two hundred years have seen a growing schism between two loosely defined schools of thought in western philosophy and this reflects also in mathematics: the empirists basing knowledge on external observations (sometimes reduced to materialism) and the idealists taking the intangible realms of pure ideas as pre-existing (apriori). The latter is of course the ancient course of spirituality and mysticism inherited in the west through Plato, Plotinus, Saint Augustine etc. and adapted to modern language and scientific rigor where possible. The empirists have their strength and victories from the times of Galileo to modern applied sciences and technology. Their merits can be more easily measured by effectiveness and money, whereas the successes of idealists are more of an esthetic nature.
This schism shows a fluctuation and competition between two major aspects of the human mind; a mentality of rational thinking sorting out sense perceptions and gravitating towards material (manas in yogic terminology) and a superior mental (buddhi) tending to the spirit and pure ideas with the help of intuition.
Both are needed for a balanced and integrated approach to science, but this unification process needs an ascending trajectory and a target that is maximally inclusive and minimally restrictive. Or simply put: infinite. Perhaps infinity (along with concepts of information, energy, vibration and resonance) will be a mutually agreeable key concept in a much needed unification of science and spirituality.
When confronting infinity or even when being just very slightly ‘touched’ by it, one may react in several ways depending where one’s ‘identity point’ is located (area or structure one identifies with):
○ If it is in the emotional and mental patterns of the ego, there is likely to arise fear triggered by the instincts for preservation of this structure,
○ whereas the soul will sense the freedom suggested by infinity and rejoice with this, and
○ the tool of the soul in the supramental (vijnanamaya kosha, the higher mental body in yoga terminology) is further awakened and filled with curiosity and sense of amazement and even hunger for intuitive understanding of the universe and ourselves and
○ the core of the soul, the most subtle layer of our manifested being, the bliss body (anandamaya kosha) will feel infinity as its subtle cosmic nourishment and essence of its happiness and bliss (ananda)
○ Beyond all these, the eternal, infinite self (atman) is at peace and at home in infinity, which is its very nature as total freedom, with its center everywhere and radius infinite, as a yogic proverb describes elliptically.
Holographic Infinity
Holographic Model
Some modern physicists, e.g. David Bohm (1917-1992) as well as the millennial tantric tradition and also alchemy consider the universe to be a gigantic hologram, where every part is reflecting the whole. The famous Tabula Smaragdina attributed to Hermes Trismegistus says: "That which is above is like that which is below, and that which is below is like that which is above, to complete the miracle of the One." Similarily, in the Bible with the words of Christ: 'I am in the Father and Father is in me'. Same is stated in Shiva Sutra 3.14 (yatha tatra tathayatra): "What is inside (of the yogi), can be found everywhere".
With the holographic model it is easier to see how the infinite can be the very 'substance' of creation from which everything is formed. A very simplified picture of Infinity versus Universe includes Maya, the cosmic illusion, seemingly ‘wrapping’ the original Infinity into something that looks like a limited thing. This infinitely gigantic trick is possibly very simple, yet extremely tricky to grasp. Let us be bold and try to imagine some simple scenarios to aid our mind and intuition in this deciphering:
Consider a ‘simple’ infinity consisting of a continuity of points in an infinite line. The size of this infinity is the above mentioned aleph-one, the size (cardinality) of the continuum.

Next we let this line make a loop with itself intersecting at one point:

We can see how the line now seems to have two parts, one infinite part (a straight line like in the beginning) connected to another part, seemingly limited forming a loop or a circle.
According to above mentioned set theories every (non-zero) part of this line contains exactly as many points as the whole line; both have the cardinality of aleph-one. Both of these parts are still infinite in size, they have aleph-one points in them - the original infinity is not diminished at all with this apparent division. For our limit-oriented mind (manas in yogic terms) these two parts seem however to be very different in size; one infinite, the other much smaller and limited. From the circle’s point of view it looks to be separated from the ‘line-world’, especially if the circle has not yet ‘realized its fullness as a circle’ and is missing the connecting point.
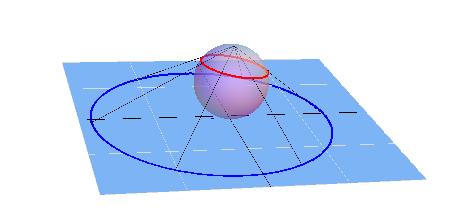
We can now make a one-to-one connection between these two parts, mapping all the points in the line to all the points in the circle (and vice versa). This mapping expresses the equality of the sizes of the two parts, their having the same cardinality (aleph-one). This mapping can be described precisely with simple trigonometric function (tangent), but here a graphical representation will suffice. We will take the point in the circle that is exactly opposite to the intersection point (I) of the circle and the line (see picture below). This will be the projection base, labeled P’. Then we draw a straight line from this projection base to any point (e.g. A or B) in the line. Where this line intersects the circle there will be the projection of that point, labeled A’ and B’ etc. We can easily see that it is possible to have such projections to all points in the infinite line and they will each have a unique projection point in the circle. Thus all of the infinite line can be uniquely (bijectively) projected or mapped on the circle. This is possible because the set of points on the circle is compact - there are always new points between any two points, in other words these points make up a continuum.

There are two special points on the circle: one where the line touches the circle (I) - this point is its own projection. The other special point is opposite it, labeled P’. This point will be mapped to the farthest point (or points) in the line - infinitely far away. Here we can think of the infinite line connecting in both 'ends' (infinitely far away) to make an infinite loop so that even this point is mapped one-to-one onto the circle (to P'). (In mathematics this is called 'one-point compactification of the real line'.)
Similar mapping can be done to any structure or process 'living' in our hypothetical one dimensional world. These structures are also preserved in this mapping. Now we have created a small microcosm that has a one-to-one correspondence to the ‘macrocosm’ of the infinite line (or circle which looks like a flat line from any finite perspective). Everything that is in the macrocosm is precisely reflected in the microcosm and vice versa. We can even suggest a yogic analogy for the the above mentioned special points relating them with brahmarandra (I), where the individual becomes tangent with the original infinity and muladhara chakra (P’), which contains projection points of the infinite line increasingly densly packed as we approach the projection base (P’), thus an infinite potential hidden like the dormant Kundalini in the base of the spine.
(This is of course a crude one dimensional analogy and not to be taken literally.)

Even the commonly used symbol for infinity contains this projection analogy, if we allow the infinite line wrap around to form another circle:

This simple one-dimensional model could be tried out in 2, 3 or 4 (space-time) dimensions or even in 11 dimensions where the strings and membranes of M-theory live and vibrate.
Also temporal cycles could be considered in a similar way, in nested loops, all of these of the same infinite timeless nature, all made of eternity.
To summarize: in this way one can imagine space-time constructions that are made of infinity itself and which have the appearance of finiteness and separateness. The mystery remains as to what is making these forms stand out from formlessness – the nature of cosmic illusion, Maya.
Let your mind rest at these ideas and images and then let your creative imagination and intuition fly from there into really feeling these infinities, melting with them, expanding in and out beyond all borders.
Further spiritual considerations – infinity breaking out of the limits of mathematics
Plotinus (205-270 BC) was following Plato’s idea that God ("the One") is infinite. He stated that The One has never known measure and stands outside of number, and so is under no limit either in regard to anything external or internal; for any such determination would bring something of the dual into it.
St. Augustine (354-430 AD) adapted Platonic philosophy to the Christian religion and he believed that God was infinite and could also think infinite thoughts. He infers that although God's power is unlimited, he still cannot make an absolutely unlimited thing, no more than he can make an unmade thing (for this involves two contradicting states being true together). One can indeed argue in general that the notion of a (totally) unlimited thing is contradictory in terms - a `thing' is by its very nature limited, defined by a process of categorization, limitation or separation from the background. Also it is logically evident that God cannot make another one equal to Him in His Totality, as that would lead to a contradiction of a 'divided totality' or 'two totalities'. But perhaps He can make 'subsets' of Him that can evolve close enough to His Uniqueness to make the identifying leap back to Him.
René Guénon (1886 – 1951) describes in his book The Multiple States of the Being (1932) in a very penetrating way some key concepts and principles of metaphysics and their relationship to infinity and mathematics.

Peter Samsel presents Guénon’s ideas in The Logic of the Absolute, The Metaphysical Writings of René Guénon:
"Guénon begins his demonstration with a primary axiom, or first principle, which he terms the Metaphysical Infinite. (…) He is careful to distinguish the Metaphysical Infinite from the mathematical infinite, which is finite, insofar as it is limited to the domain of numbers. The Metaphysical Infinite is simply that which has no limits of any kind. Several necessary characteristics follow upon this essential definition: The Infinite is without any limitation, restriction, or determination, for any such would clearly contradict its infinitude. It is unique, all-encompassing, and an absolute Totality, for if anything were exterior to it, it would not be the Infinite. It is without parts, for any part would be relative and finite and could thus have no common measure or relationship to it. It is absolutely indeterminate, as any positive definition would serve as a delimitation, and thus could not apply to it. By the same measure, it is absolutely affirmed, as its indetermination—the negation of any limiting definition—is equivalent to the negation of negation as such and thus total affirmation. Finally, it is incontestable, as its absolute indetermination implies that it cannot be defined, discussed or, for that matter, contested. The essentially apophatic definition of the notion of the Metaphysical Infinite implies also that, just as it cannot be rationally contested, so it is not open to rational proof. Rather, another mode of discernment must be appealed to, one that might be termed “intellectual intuition.” (Peter Samsel, 2006, emphasis added)If our mind is open, this kind of reasoning (springing from the heart) can even convince the mind of the necessity of this original, undefinable Infinity. If we do not confine ourselves to any apriori limitations of Reality (in the maximally extensive sense of the word), our mind is forced to accept this absolute affirmation of the Metaphysical Infinite.
Here we are not only in the heart of mathematics, but also in the heart of philosophy. In the true sense of the word, a philosopher is a lover of Truth (Philo+Sophia). Just as a man deeply in love with a woman, sees her as an embodiment of Absolute Beauty, Creativity, Freedom, Joy etc., so does a true philosopher behold Truth: beyond all limitations, Absolute and Pure. There is no other possible way for the Truth to be, anything else would be incomplete and inconceivable. But it is our heart that must burn for this lover (Sophia), while our mind surrenders and accepts the role it originally had; a divine scribe formulating love letters of philosophical or mathematical investigations for our lover, however incomplete these letters unavoidably are.
Cantor was sharing a similar view to Guénon, that Absolute Infinity is totally unlimited and thus totally beyond definitions. Yet Guénon is pointing beyond all possible limiting concepts, including the concept of number, thus going beyond counting, beyond one/many dualism. One could perhaps perceive how the mathematical 'absolute limit infinity', great Omega, Ω - absolute in the category of numbers - is a kind of platonic idea or 'manifestation' of Metaphysical Infinity in the ideal universe of numbers.
Guénon is introducing another aspect of Metaphysical Infinity for us to understand how this Infinity can be active and creative. Infinity ‘opens’ in what he calls Universal Possibility (similar to the Infinite Potential in David Bohm's theory of Implicate Order).
Everything that is not contradicting itself finds its life in this absolutely free and unlimited realm. This is strikingly similar to the tantric concept characterizing the essence of Cosmic Consciousness; Svatantrya, perfectly free Will and perfect unlimited spontaneity (see e.g. Kashmir Shaivism). Metaphysical Infinity together with Universal Possibility resemble the related pair of concepts in non-dual shaivism, namely Prakasha and Vimarsha, uncreated light and its reflection (through Svatantrya) and expression in itself, both perfectly united together yet whispering the most subtle idea of dualism anticipating manifestation. Within this Universal Possibility some ‘things’ are possible to manifest, others not, both categories being in the unmanifest sphere. Manifestable possibilities can then further take shape to become manifested in time and space and be conditioned by limitation and change, still keeping their essence in the transcendent realm of infinite possibilities.
According to Guénon the purpose of man is to realize the Metaphysical Infinite through his integrated and total Being that will fully participate in the Universal Possibility thus overcoming his limited individuality.
Touching the Void
When one zooms into a fractal image, for example a graph iterating a Mandelbrot set, in addition to vertigo, one can get a sense of an ineffable infinite void which is opening with the form of the emerging transcendental entity. Form and emptiness intertwine and merge like described in the Heart Sutra ("Form is Emptiness and Emptiness is Form"). Coming back to mathematics, we can think of zero (the origo) as representing the Original Void, the source of everything ("The Creative Void") and Infinity as the destiny of everything ("All-absorbing and All-synthesizing Void") - together like "the Alpha and Omega". We can even calculate how infinity and zero are working together and characterizing each other in the equations: 1/x → ∞ as x → 0 and 1/x → 0 as x → ∞ (inverse of x tends to infinity as x tends to zero and vice versa). Already Leibnitz noticed this extraordinary couple and Guénon was naming a counterpart to his Metaphysical Infinity as the Metaphysical Zero, from which the mathematical zero is derived as a kind of practical operator, originally not really being a number (like infinity). Creation and dissolution are an interplay of these two metaphysical entities, very much like between Prakasha and Vimarsha (between pure Consciousness and its Reflection in the Absolute Freedom of the Void) as described in Kashmir Shaivism (also referred to as Shiva and Shakti, the two essential facets of the Undefinable One).

Reflection Principle
Modern number theories are based on set theories, which usually contain some form of reflection principle stating that for every attribute of the whole (collection of all sets) there can be found a set with this same attribute. If contrary were true we could find an attribute that is not valid for any parts and this attribute could then be used to define whole as separate from all of its parts. When Whole refers to Everything this would be counterintuitive as Whole must be considered beyond all limiting definitions (otherwise these limits would point to something outside of this Whole) and more than its parts together. Neither can Whole be defined by just summing up the attributes from all parts, which would always leave something missing.
However, not all properties can be applied as attributes to the reflection principle, for example the quality of being the collection of all sets is not shared by any set. Whole is One without another. There can be only one Whole, otherwise it would not be Whole, all-inclusive.
Applying reflection principle we can try to deduce an answer to the question: 'Does creation contain actual infinities?'
God is Infinite.
(reflection principle =>)
There is a 'subset of God' which is infinite.
Therefore there are infinite things which are from God.
But the 'subsets of God' with this attribute of infinity need not to be manifested. Perhaps they are somewhere between God and manifestation, e.g. within the pure tattvas of shaivistic ontology or as logoi (logos), pure thoughts, pure intentions.
On the other hand we can simply realize that everything created is made out of the same original Infinity (as nothing else exists in the first place - or better said: everything is initially totally unlimited, infinite) so that this Infinity is still present in everything, although hidden from the mind that works only with limits. From infinity nothing but infinity can come forth, rest is just an illusion. We only need to see this clearly and let go of those suggestions in our mind that insist otherwise. Then we can wholeheartedly and freely partake in this mysterious game of illusion (lila, in sanskrit) without getting caught in it.
To see a World in a Grain of Sand And a Heaven in a Wild Flower Hold Infinity in the palm of your hand And Eternity in an hour - Auguries of Innocence, William Blake
Some 'parts' of Infinity let their infinite nature be revealed more easily. It is much harder to expand indefinitely contemplating on attributes that characterize our limited mind, like egoism, attachment to form, pain, fear, ignorance etc. We need to focus on something thas has infinity as its essence, like our eternal divine self (atman), or on attributes like total freedom, unconditional love, pure uncreated white light or other attributes of an infinite nature. Yet focusing on infinity is just a starting point in this type of jnana yoga (infinity yoga). A further step consists of deeper and deeper identification with infinity, finally becoming one with infinity.
"But the greatest of these is love"
During these steps jnana yoga necessarily needs to unite with another type of yoga to carry over the abyssal spaces. This type of yoga is traditionally called bhakti yoga. Practically this involves recognizing in the nature of infinity something fundamental we desire and love, e.g. our original, essential freedom and love itself, unconditional, unlimited. Now our contemplation of infinity is supported by an ever increasing impetus from our heart. This process may autocatalyze, fueling itself (to the point our structure can support), because we are essentially opening our being to receive more and more of the liberating Grace, the mysterious, all-powerful energy from Absolute Infinity itself that is always available for us, always waiting for us to open ourselves to it.
As a tantric proverb says: "When love becomes infinite, the impossible becomes easily possible".
Taking into account the holographic nature of creation through infinite subsets sharing the same cardinality as the Infinite Whole, a stronger version of reflection principle might be valid for some attributes: All holographic subsets of infinity (subsets that preserve the cardinality of that original infinity) share the essential attributes of that infinity. Some of these essential attributes are the Godly Attributes that are often exemplified for us in the meditations supported by Gregorian Bivolaru, the founder of the yoga school MISA (Natha's sister school). These Godly Attributes include the 'classical' ones: Godly Omnipresence, Godly Omniscience, Godly Omnipotency and Godly Omnitemporality (Godly Eternity, Godly Simultaneity, Godly Moment) plus many, many others like Godly Love, Godly Synthesis, Godly Good, Godly Harmony, Godly Unity etc. In yogic terms these Godly Attributes are mysteriously shared by Paramatman (God) and atman (our infinite, eternal self), Whole and its reflection. By resonating more and more with these Godly Attributes we can open up to the Infinity within and to that which Cantor called Absolute Infinity and Guénon called Metaphysical Infinity - the Infinity and total Freedom of God.
Note: Some of the concepts and methods mentioned in this article can be studied and practised in the Esoteric Yoga and Tantra courses of Natha and other Atman schools, and especially in the Kashmir Shaivism course.